Models and the Scientific Method
Contents
Models and the Scientific Method¶
The Scientific Method or the Data Science Life Cycle?¶
This section will describe the steps involved in the lifetime of a project in data science.
The scientific method roughly follows a cycle of asking questions, designing an experiment to model the world, and use the results of this experiment to assess if the experiment answered the question at hand. Results feed into more questions, or a refinement of the approach when results are inconclusive.

This description hides a much more complicated process that drives any realistic scientific investigation. In particular, this glosses over:
time spend understanding and investigating the domain or area in question,
data may not be collected by experiment; existing data must be found,
the experiment may involve complicated assumptions, as well as mathematical and statistical modeling,
The results of the experiment may not clear-cut and may involve subtle statistical interpretation.
Information gained at any step may result in stopping progress to further research and reformulate the question.
A diagram more realistically describing this process is more complicated:
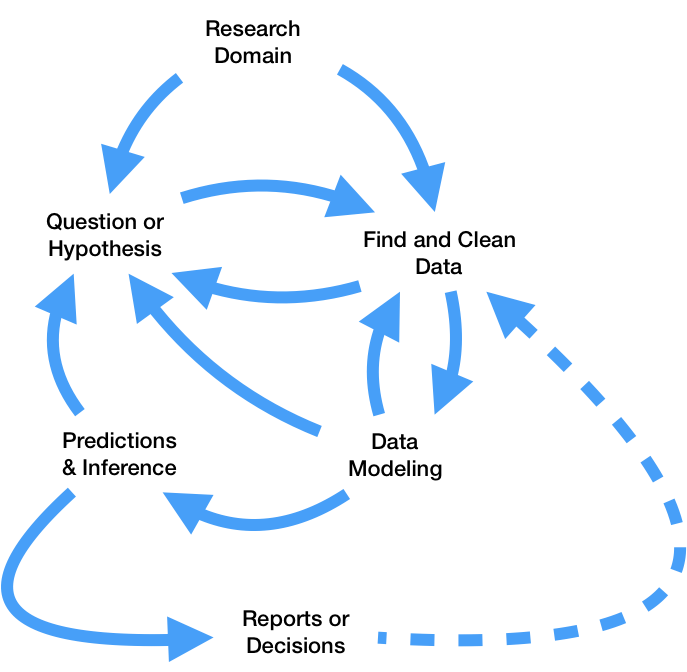
Any involved, real-world project is a complicated, iterative process. As a Data Scientist, it’s important to understand each component well to maintain one’s bearings, know how to correctly interpret results, and quickly iterate through refinements of each question being pursued. Navigating this diagram requires understanding the logical and statistical arguments involved in each step, as well as the software that executes these arguments.
Introduction to Models¶
A few important terms will be used in the text to describe how the various steps in the diagrams above relate to one another:
The true or conceptual model is the representation of a system in a domain that captures a question of interest.
A data generating process is the physical process from which the true model creates the observed data. These processes involve complicated unknowns that cannot necessarily be observed or explicity modeled.
A probability model is an idealized, simplified explanation of the data generating process. The model is probabilistic, as it must capture perceived randomness in the data generating process.
An instance of Observed data is a real world manifestation of the data generating process, recorded as a dataset.
A (fit) statistical model is the most likely explanation of what a probability model is in terms of the observed data.
