Contents

Creating Modeling Pipelines

Creating Modeling Pipelines

Building a statistical model requires developing the following steps:

  1. Create features to best reflect the meaning behind the data,

  2. Choose a model that captures relationships between features,

  3. Select a loss function and fit the model,

  4. Evaluate the model using the appropriate notion of error.

Once these steps are completed, the model can be used for prediction or inference.

Each of these steps may contain complicated transformations and logic, often involving thousands of choices among which parameters and features are most effective. Data pipelines handle this complexity, keeping track of these myriad choices in a organized fashion.

Modeling Pipelines in Scikit-Learn

Models in Scikit-learn are defined as Estimators. The Estimator class is similar to the Transformer class for generating features. The Estimator class implements the following interface:

  • Estimator.set_params defines parameters needed for fitting the model.

  • Estimator.fit(X, y) fits the model on the features X and the target variable y.

  • Estimator.predict(X) returns predictions for observations in X from the fit model.

  • Estimator.score(X, y) returns an evaluation of the fit model on data X and target y.

    • A custom evaluation metric may be specified to generate the score.

    • For classifiers, the default score is the accuracy.

    • For regressors, the default score is the coefficient of determination (\(R^2\)).

Remark: The Estimator class is similar to the transformer class. The main difference is the presence of the target variable y. In fact, a fit model behaves like a transformer, where predict corresponds to transform.

Example: Fitting a multivariate regression model is straightforward using Estimators. Below is a small dataset with two independent variables (x1 and x2) and one target variable y.

data
x1 x2 y
0 -9.623415 -0.991037 -19.420887
1 -9.109035 -1.145796 -17.835602
2 -8.583274 0.885662 -14.760810
... ... ... ...
17 4.246154 2.712184 15.964720
18 4.759243 4.643905 17.381630
19 5.121245 3.419691 21.253360

20 rows × 3 columns

A linear regression is fit on the variables and target:

from sklearn.linear_model import LinearRegression

y = data['y']
X = data.drop('y', axis=1)

lr = LinearRegression()
lr.fit(X, y)

The RMSE and \(R^2\) are computed as follows:

np.sqrt(np.mean((lr.predict(X) - y)**2)) # RMSE

2.1591119732981725

lr.score(X, y) # R^2

0.9689164664534166

The plane of best-fit is visualized below:

plot3Dscatter(data, 'x1', 'x2', lr, data['y'])
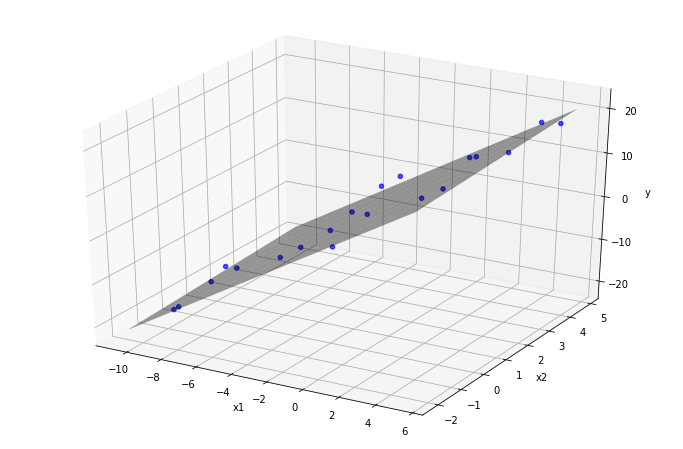
../../_images/model-building_11_0.png

The regression coefficients are contained in the coef_ attribute; the coefficients are the slopes of the projection of the plane of best fit onto the x1-y-plane and the x2-y-plane respectively.

lr.coef_

array([2.4586771 , 0.33546627])

Other estimators have parameters that must be passed into the constructor.

Example: A k-nearest neighbor regressor finds the makes predictions by averaging the y-values of the k-nearest examples to a given data point. The example below fixed the number of neighbors at 3:

from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=3)

After fitting the model, it predicts new possible outcomes on out-of-sample data:

knn.fit(X, y)
test_data = np.array([[1.0, 2.0]])
knn.predict(test_data)

array([8.87123925])

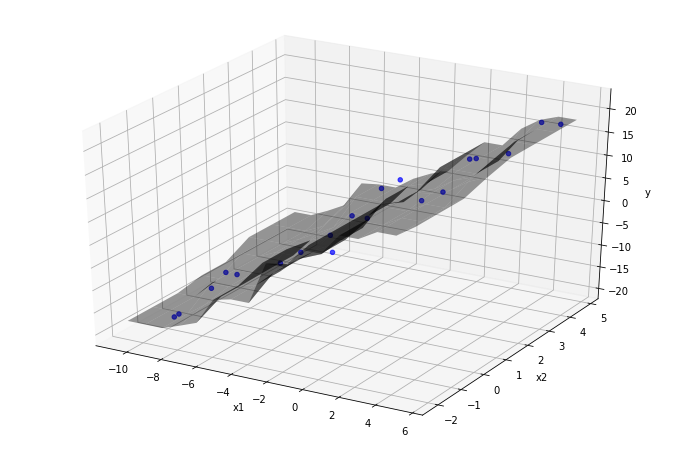
The prediction function is visualized as a function of two variables, alongside a scatter-plot of the training data. Every point on the surface is calculated by averaging the value of the nearest three data-points:

plot3Dscatter(data, 'x1', 'x2', knn, data['y'])
../../_images/model-building_19_0.png

Using Estimators in Scikit-Learn Pipelines

Scikit-learn pipelines may contain Estimators as the final step. As with pipelines composed of transformers, a pipeline containing an estimator is itself an estimator.

For example, calling pl.fit(X, y) on a pipeline pl = Pipeline(steps) containing an estimator roughly executes the following logic:

out = X
for step in steps[:-1]:
    out = step.fit_transform(out)

step[-1].fit(out, y)

Similar logic applies to the predict and score methods.

Example: The dataset below contains home sales in Ames, Iowa compiled by Dean De Cock. The variables consist of a mixture of categorical and quantitative variables that describe the characteristics of each home in the dataset. A simple question one might ask:

Can the price of the home sale be predicted from the characteristics of the house?

Approaching this question thoroughly is involved. This example merely constructs a basic pipeline with the following properties:

  • Missing values in quantitative variables are imputed with the value 0, then passed directly to the model without further feature engineering. Imputing with 0 is reasonable, as all quantitative columns with missing values represent positive quantities.

  • Categorical variables are treated as nominal, imputed with the string NULL, then one-hot encoded. This attempt at feature engineering is a bare minimum and serves only as a baseline upon which to improve.

  • The model chosen is a ‘Decision Tree Regressor’, which is well-suited to the features above.

# required imports
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import FunctionTransformer
from sklearn.impute import SimpleImputer
from sklearn.tree import DecisionTreeRegressor
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline

The housing data consists of 1460 observations (houses) and 81 attributes: one ‘Id’ column that identifies the distinct houses, the target variable ‘SalePrice’, and 79 features:

housing = pd.read_csv('data/housing.csv')
housing
Id MSSubClass MSZoning LotFrontage LotArea Street Alley LotShape LandContour Utilities ... PoolArea PoolQC Fence MiscFeature MiscVal MoSold YrSold SaleType SaleCondition SalePrice
0 1 60 RL 65.0 8450 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 2 2008 WD Normal 208500
1 2 20 RL 80.0 9600 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 5 2007 WD Normal 181500
2 3 60 RL 68.0 11250 Pave NaN IR1 Lvl AllPub ... 0 NaN NaN NaN 0 9 2008 WD Normal 223500
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1457 1458 70 RL 66.0 9042 Pave NaN Reg Lvl AllPub ... 0 NaN GdPrv Shed 2500 5 2010 WD Normal 266500
1458 1459 20 RL 68.0 9717 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 4 2010 WD Normal 142125
1459 1460 20 RL 75.0 9937 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 6 2008 WD Normal 147500

1460 rows × 81 columns

Dropping the ‘Id’ field and removing the ‘SalePrice’ as the target variable:

X = housing.drop(['Id', 'SalePrice'], axis=1)
y = housing['SalePrice']

The categorical and quantitative columns are gathered into lists of column names:

types = X.dtypes
cat_cols = types.loc[types == np.object].index
quant_cols = types.loc[types != np.object].index

The pipeline described above is put together:

# categorical features
cat_process = (
    'cat_processing',
    Pipeline([
        ('imputer', SimpleImputer(strategy='constant', fill_value='NULL')), 
        ('one-hot', OneHotEncoder())
    ]),
    cat_cols
)

# quantitative features
num_process = (
    'num_processing',
    SimpleImputer(strategy='constant', fill_value=0),
    quant_cols
)

ct = ColumnTransformer([cat_process, num_process])

# modeling pipeline
pl = Pipeline([('features', ct), ('regressor', DecisionTreeRegressor(max_depth=3))])

After fitting the pipeline, the RMSE can be calculated:

pl.fit(X, y)

preds = pl.predict(X)

np.sqrt(np.mean((preds - y)**2)) # RMSE

40142.374455005905

previous

Introduction to Modeling

next

Bias and Variance